用 Python 实现一个二分查找的函数。

二分查找几乎是算法面试里的常客。它的本质是“在有序空间里对半缩小不确定区间”，时间复杂度 O(log n)、空间 O(1)，实现却常被边界细节绊倒。下面用通俗的方式把二分查找讲清楚：先给出最常用的迭代版本，再补充递归写法与“查左边界/右边界”的实战模板，最后用若干例子收尾。

场景：给定升序数组 nums 和目标值 target，若存在则返回其任意一个下标，否则返回 -1。

思路很直接：维护闭区间 [l, r]，每次取中点 m；若 nums[m]==target 返回；若 nums[m]<target，说明目标在右侧，l=m+1；反之 r=m-1。循环条件用 while l <= r，确保区间不漏检。

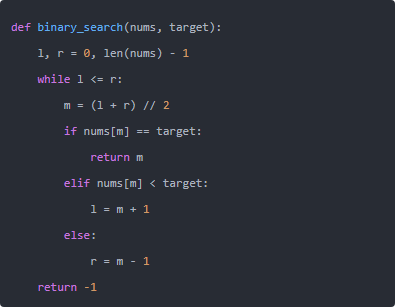
这段代码是最常用的“命中即返”版本，适合元素互不相同或不关心“返回哪一个”的情况。

时间复杂度 O(log n)，空间 O(1)。 Python 不存在整型溢出问题，(l + r) // 2 安全；但在某些语言里需写成 l + (r - l) // 2 避免溢出。

递归表达逻辑更直观，但 Python 默认递归深度有限，大数组上不如迭代稳妥。

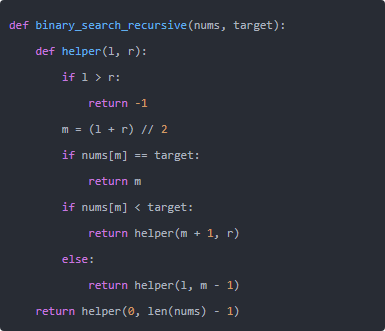
很多业务并不满足“随便找一个”，而是要“第一个等于 target 的位置”（左边界）或“最后一个等于 target 的位置”（右边界）。这时候经典的做法是把“相等”也当作继续收缩的一侧，从而逼近边界。

左边界（lower_bound）：第一个 ≥ target 的位置

如果只关心“是否存在”，判断 idx < n and nums[idx] == target 即可；要精确到“第一个等于”，这个位置就是答案。

若要“第一个等于 target”的下标：

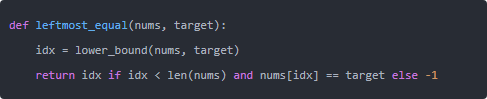
右边界（upper_bound-1）：最后一个 ≤ target 的位置

上界（upper_bound）是“第一个 > target 的位置”，于是右边界 = upper_bound - 1。

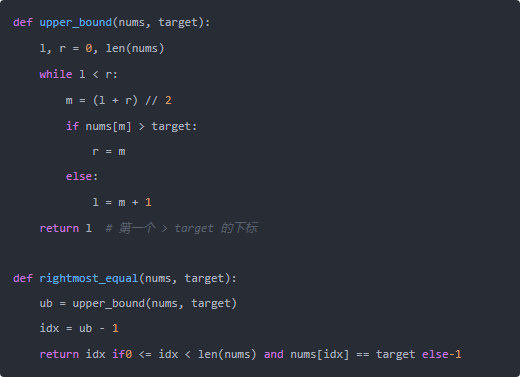
这种“半开区间 + 上下界分离”的写法非常稳健，几乎覆盖所有重复元素场景。记住两个判定：

lower_bound：遇到 >= target 往左收缩；upper_bound：遇到 > target 往左收缩；否则往右。

循环条件与区间定义要匹配

闭区间 `[l, r]` 用 `while l <= r`，更新为 `l = m + 1` 或 `r = m - 1`。 半开区间 `[l, r)` 用 `while l < r`，更新为 `r = m` 或 `l = m + 1`。 

避免死循环 每次更新必须严格缩小区间；比如半开区间里，r = m（不是 m - 1），因为右端本来就排除 r。 空数组与越界lower_bound 可能返回 len(nums)；使用前先判 idx < len(nums)。 重复元素的“等于”归属 想要左边界，== target 应归入“往左收缩”的分支；想要右边界则相反。

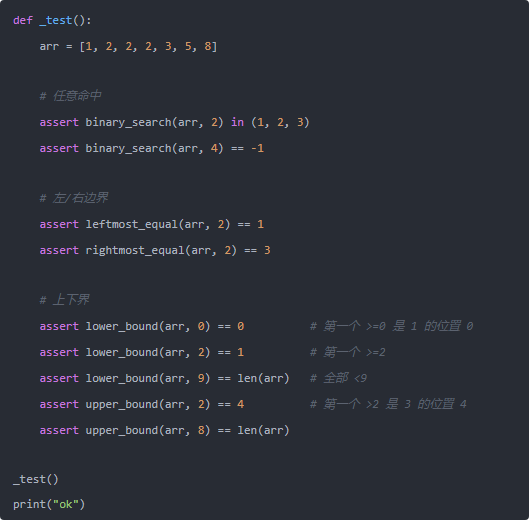
记住一句口令就好：确定区间开闭，明确比较方向，保证区间严格缩小。

要任意命中：命中即返；小于去右，大于去左。 要左边界：把“相等”并入“向左”那侧；要右边界则相反。 用半开模板 [l, r) 可以降低越界焦虑，while l < r，r = m / l = m + 1。

很多面试会追问“如果找不到，返回应该插入的位置”。这其实就是 lower_bound 的返回值。比如在保持有序的前提下插入 target：

当 target 已存在时，它返回的是“第一个等于”的位置（左边界）；不存在时，则是“应该插入”的位置。与标准库 bisect_left 行为一致。

统计区间频次：等于 x 的元素个数 = upper_bound(x) - lower_bound(x)。 去重/去重计数：用下界、上界快速定位连续段。 答案单调的决策问题：例如“最小可行值”“最大可行值”，把可行性判定封装为单调布尔函数，再用二分在答案空间里搜解。

二分查找不难，但“边界开闭 + 等号归属 + 区间收缩”这三件事要想透。迭代版稳健、递归版清晰；处理重复元素时，养成用 lower_bound/upper_bound 模板的习惯，几乎不会翻车。掌握这些，你在面试里既能写出无 bug 的代码，也能把思路讲得让人信服。

以上就是“用 Python 实现一个二分查找的函数。”的详细内容，想要了解更多Python教程欢迎持续关注编程学习网。