你必须了解的十大「统计常识」！

统计，已经成为了一门必修课，无论你在什么行业。

在商业决策高度依赖数据分析的今天，如果没有较好的统计知识储备，是很难去理解和分析数据的。然而在广袤无际的统计知识里，哪些是最有必要掌握的基础、哪些最经常被商业界用到？我们整理了十个非常重要的统计概念，它们是所有高阶统计知识的基础，也是学生和打工人最有必要了解的统计知识。赶快来看看吧！

1.总体与样本
总体是研究对象的整个群体。比如，“美国大学生“这个“总体”是所有在美国的大学生的集合；欧洲25岁的人是所有符合该描述的人的集合。由于我们很难去收集总体的所有数据，所以对总体进行分析并非总是可行的。因此，我们开始使用样本。样本是总体的子集。 例如，我们没法对所有美国大学生进行调查研究，那么我们就从中抽出1000名美国大学生，这1000名美国大学生就是“美国大学生总体”的子集。 2.正态分布
概率分布是表示某事件或实验结果的概率的函数。比如数据框中的某一列，它是一个变量，其概率分布函数表示里面不同数值出现的可能性。概率分布函数在预测分析或机器学习中非常有用，我们可以根据该样本的概率分布函数对总体进行预测。
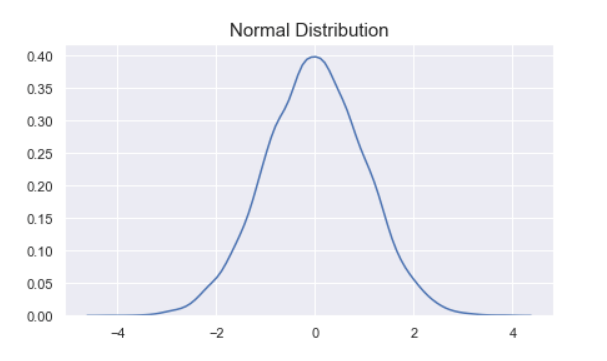
正态（高斯）分布是呈现“钟形”的概率分布函数。下图是典型的正态分布曲线的形状，这条曲线是通过NumPy的numpy.random.randn函数返回的随机样本生成的。 

曲线峰值表示变量最可能出现的数值。数值离峰值越远，出现的概率越低。下图更严谨地展示了正态分布：百分比表示一个随机的观测值落在该区域的可能性。离均值越远，我们可以看到更多的极端值，而观察到的可能性就越小。举一个例子，如果全球的成年男性的身高呈正态分布，总体的平均身高为170厘米，那么当我们随机选择一位成年男性并测量其身高时，我们就有68%左右的可能性抽到了一位身高是在距离170厘米一个标准差之内的成年男性。

3. 中央趋势的度量 中央趋势是一个概率分布的集中（或典型）值。最常见的测量中央趋势的方法是平均值、中位数和众数。中央趋势能从某种角度上描述和概括一组数据的特征。

• 平均值：数列的平均值。

• 中值：当数列以升序或降序排序时位置在中间的值。

• 众数：出现最多的值。

4. 方差和标准差
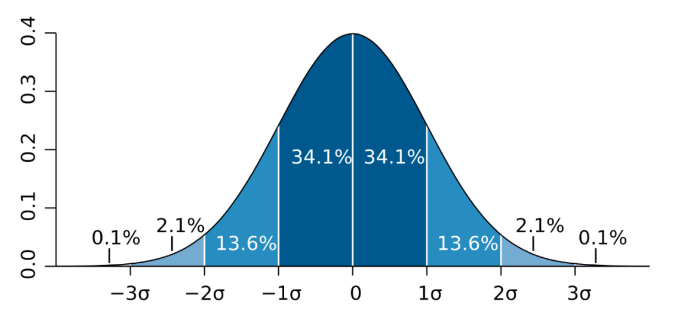
方差描述的是一组数据中心偏离的程度，用来衡量一批数据的波动大小（即这批数据偏离平均数的大小）。在样本容量相同的情况下，方差越大，说明数据的波动越大，越不稳定。举个通俗易懂的例子，如果A同学一年中的考试成绩的方差比B同学大，那么说明A同学的考试成绩波动较大。但这并不说明A同学成绩一定比B同学差，因为B同学的考试成绩可能是稳定地较低。所以方差并不能全面概括一组数据的特性，还需要结合其他的指标（比如中央趋势），才能让我们较为了解数据的全貌。

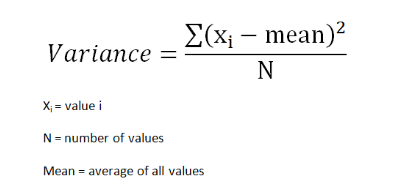
标准差衡量的是数据的离散程度，它是方差的算数平方根。 注：平均值，中位数，众数，方差和标准差是基本的描述统计量，有助于解释变量。

 5. 协方差和相关性      协方差用于衡量两个变量变化趋势的相互匹配程度。通俗地讲，就是两个变量在变化过程中是同方向变化？还是反方向？同向或反向程度如何？

具体来讲，协方差根据两个变量离均值（或期望值）的偏差来比较两个变量。下图展示了随机变量X和Y的部分值。橙色点表示变量的平均值，其他值相对于平均值以相同的趋势变化，因此，X和Y的协方差为正。

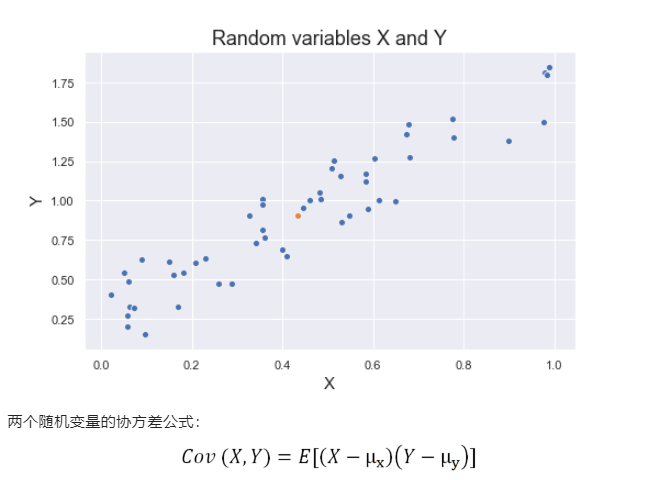
其中E为期望值，μ是平均值。 注：当两个变量相同时，协方差即是方差。

不过协方差的值的大小，会收到变量量纲的影响。什么意思？就是当两个变量的变化幅度很大时，那么它们之间的协方差就会很大。所以协方差并不能纯粹地测量出两个变量每单位变化时的相似程度。那么怎样才能去除量纲的影响呢？相关系数就横空出世了！ 

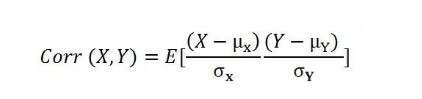
相关系数，说白了就是从协方差中剔除数据变化幅度的影响，这个变化幅度如何剔除呢？其实就是在公式中引入对标准差的剔除。

标准差描述了变量在整体变化过程中偏离均值的幅度。协方差除以标准差，也就是把协方差中变量变化幅度对协方差的影响剔除掉，这样协方差就标准化了，它反映的就是两个变量每单位变化时的情况，这也就是相关系数的公式含义了。你可以想象一下：当X或Y的波动幅度变大的时候，它们的协方差会变大，标准差也会变大，这样相关系数的分子分母都变大，其实变大的趋势会被抵消掉，变小时也是亦然。于是，相关系数不像协方差一样可以正无穷到负无穷之间变化，它只能在+1到-1之间变化。
 6.中心极限定理 在包括自然科学和社会科学在内的许多领域中，当我们不知道随机变量的分布时，就会使用正态分布。中心极限定理（CLT）证明了在这种情况下使用正态分布的合理性。根据中心极限定理，随着样本量的增加，无论总体分布如何，样本平均值将趋向于正态分布。
假设我们想知道一个国家所有20岁年轻人的身高分布，要收集所有的数据几乎是不可能的。因此，我们可以对全国20岁的人群进行抽样，并计算出样本中的平均身高。中心极限定理指出，当我们从总体中抽取的样本越来越多，样本分布将接近于正态分布。
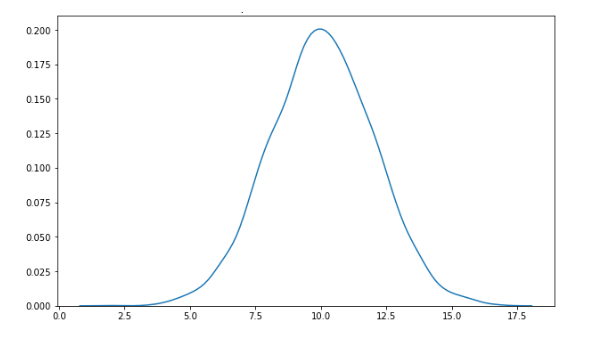
为什么正态分布如此重要？因为正态分布可以用均值和标准差表达出来，并且可以很容易地计算出来。而且，如果我们知道一个正态分布的均值和标准差，就可以计算出关于它几乎所有的统计量。 7.P值 P值是一个随机变量取某个值的可能性。假设有一个随机变量A和值x，x的p值是A等于x或等于具有相等或更少几率被观察到的任何值的概率。下图是A的概率分布，从图中可以看出我们很可能观察到一个10左右的值。但随着数值变得更高或更低，我们能观察到该值的概率越低。

假设有另一个随机变量B，我们想要知道B是否大于A。B的平均样本均值是12.5，12.5的p值是下图中的绿色区域。绿色区域表示A为12.5或大于12.5的可能性。

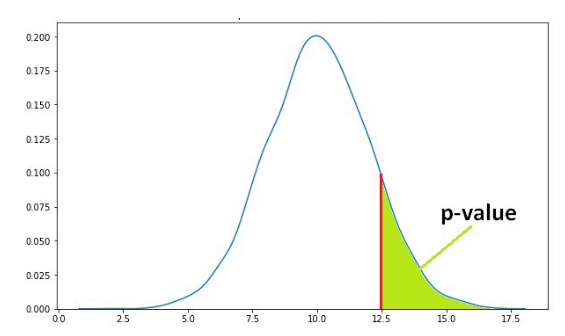
如果p值为0.11，那如何解释呢？p值为0.11意味着：我们对结果有89％的把握，也就是说当我们做无数次观测、得到了无数个B的样本，我们观测到的B的样本均值有89%的几率是大于A的，有11%的几率是随机误差造成的。当随机误差的几率低于5%的时候，也就是p值小于等于0.05时，我们一般认为这种差异是统计性显著的。

注意：p值越小，结果的确定性越高。如果随机变量B的样本均值的平均值为15（更极端的情况），则p值将小于0.11。
8. 随机变量的期望 随机变量的期望是该变量所有可能值的加权平均值，这里的权重是指随机变量为特定值的概率。离散型和连续型随机变量期望值的计算方式有所不同：

• 离散型随机变量的取值可以是有限个或者可数无穷个。比如一年中的雨天的数

  量就是一个离散型随机变量。

• 连续型随机变量的取值不可以逐个列举出来，且可以有无穷个。例如，从家到

  办公室所花费的时间就是一个连续型随机变量，根据不同测量方式（分钟，秒，

  纳秒等）它可以取无穷个不可列举的值。

9. 条件概率 概率反映随机事件出现的可能性大小，在 0到1之间取值。事件A的概率表示为p（A），是期望出现的结果数占所有结果数的比重。比如，掷骰子时，得到小于3的数字的概率为2 /6，其中期望得到的结果数为2个（1和2），所有可能出现的结果数为6。
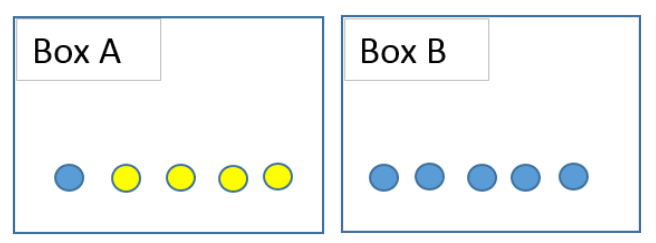
条件概率是在另一个与事件A相关的事件已经发生的条件下，事件A发生的可能性。如下图所示，假设我们在两个盒子中放置了6个蓝球和4个黄球。如果随机挑选一个球， 拿到一个蓝球的概率是6/10 = 0.6。那么如果是从盒子A中取一个球呢？捡到蓝球的可能性明显降低。这个“从盒子A中挑选”的条件改变了事件发生的可能性（取一个蓝球）。在事件B发生的条件下A发生的概率表示为p（A | B）。

10.贝叶斯 根据贝叶斯定理，可以使用事件A和事件B的概率以及事件B在A发生的情况下的概率来计算B发生情况下事件A的概率。 

贝叶斯定理非常基础且很常用，并且还有一个称为“贝叶斯统计”的领域。在贝叶斯统计中，一个事件或假设的概率可以作为已知的证据或信息。因此，先验概率和后验概率因为已知信息的不同而区分开来。

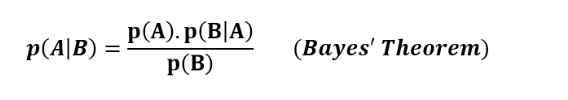
朴素贝叶斯算法是通过结合贝叶斯定理和一些朴素的假设构建起来的。在朴素贝叶斯算法中，我们假设数据中的各个特征彼此独立，且它们之间没有相关性。 

结论 

本文中我们已经涉及了一些基本但又很重要的统计概念，如果你正在或将要在数据领域工作与学习，那么很可能会遇到这些概念。当然，统计相关的知识还有很多，但一旦了解了基础知识，就可以进一步去学习更高层次的知识。

以上就是“你必须了解的十大「统计常识」！”的详细内容，想要了解更多IT圈内资讯欢迎持续关注编程学习网